阅读下列说明和数据流图，回答问题1至问题3，将解答填入对应栏内。

 [说明]

 某供销系统接受顾客的订货单，当库存中某配件的数量小于订购量或库存量低于一定数量时，向供应商发出采货单；当某配件的库存量大于或等于订购量时，或者收到供应商的送货单时并更新了库存后，向顾客发出提货单。该系统还可随时向总经理提供销售和库存情况表。

 以下是经分析得到的数据流图及部分数据字典，有些地方有待填充，假定顶层数据流图是正确的。图1-1是顶层数据流图，图1-2是第0层数据流图，图1-3是第1层数据流图，其中(A)是加工1的子图，(B)是加工2的子图。

 [图1-1]

  

 [图1-2]

  

 [图1-3]

  

 [数据字典]

 (1)数据流条目

 订货单=配件号+配件名+规格+数量+顾客名+地址

 提货单=订货单+金额

 采货单=配件号+配件名+规格+数量+供应商名+地址

 送货单=配件号+配件名+规格+数量+金额

 (2)文件说明

 文件名：配件库存

 组成：{配件号+配件名+规格+数量+允许的最低库存量}

根据题意，图1-2中哪个文件可不必画出。

(5)

(4)

(2)

(3)

(5)

阅读以下说明和C代码，将应填入(n)处的字句写在对应栏内。

 [说明]

 函数combine(a，b，c)是计算两个整数的组合数。由于计算结果可能超出10ng整型的可表示范围，故采用数组方式存储，例如：k位长整数m用数组c[]存储结构如下：m=c[k]×10^k-1+c[k-1]×10^k-2+…+c[2]×10+c[1]，利用c[0]存储长整数m的位数，即c[0]=k。数组的每个元素只存储长整数m的一位数字，长整数运算时，产生的中间结果的某位数字可能会大于9，这是就应该调用format将其归整，使数组中的每个元素始终只存储长整数的一位数字。

 整数a和b(a＞b)的组合数为：，其中u1=a，u2]=a-1，…，ub=a-b+1，d1=1，d2=2，…，db=b。为了计算上述分式，先从u1，u2，…，ub中去掉d1×d2×…×db的因子，得到新的u1，u2，…，ub，然后再将它们相乘。

 [函数]

 #define NAXN 100

 int gcd(int a，int b)//求两个整数a和b的最大公因子

 {

 if(a＜b){

 intC=a；a=b；b=c；

 }

  for(inti=b；i＞=2；i--){

 if( (1) )return i；

 }

 return 1；

 void format(int *a)//将长整数数组归整

 {

 int i；

 for(i=1；i＜a[0]||a[i]＞=10；i++){

 if(i＞=a[0]) (2)；

 a[i+1]+=a[i]/10；

 a[i]=a[i]%10；

 }

 if(i＞a[0]) (3)；

 }

 void combine(int a，int b，int *C)

 {

 int i，J，k，x；

 int d[MAXN]，u[MAXN]；

 k=0；

 for(i=a；i＞=a-b+1；i--)u[++k]=i；

 u[0]=b；

 for(i=1；i＜=b；i++)d[i]=i；

 for(i=1；i＜=u[0]；i++){//从u中各元素去掉d中整数的因子

 for(j=1；j＜=b；j++){

 x=gcd(u[i]，d[j])；//计算最大公约数

 u[i]/=X；

 d[j]/=x；

 }

  (4)；C[1]=1；//长整数c初始化

 for(i=1；i＜=u[0]；i++)(//将u中各整数相乘，存于长整数c中

 if(u[i]!=1){

 for(j=1；j＜=c[0]；j++){

 C[j]=(5)；

 }

 format(C)；//将长整数c归整

 }

 }

 }

(1)

(4)

(3)

(2)

阅读以下说明和Jrdva代码，将应填入(n)处的字句写在对应栏内。

 [说明]

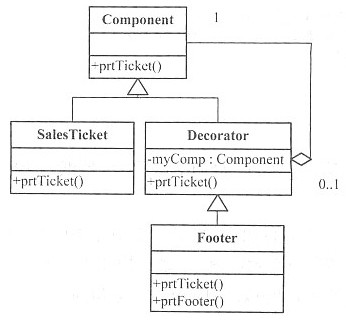
 在销售系统中常常需要打印销售票据，有时需要在一般的票据基础上打印脚注。这样就需要动态地添加一些额外的职责。如下展示了Decorator(修饰)模式。SalesOrder对象使用一个SalesTicket对象打印销售票据。图6-1显示了各个类间的关系。以下是Java语言实现，能够正确编译通过。

 [图6-1]

 [Java代码]

 //Component.java文件

 public (1) class Component {

 abstract publ ic void prtTicket()；

 }

 //salesTicket.java文件

 public class SalesTicket extends Component{

 public void prtTicket(){

 //Sales ticket printing code here

 System.out.printin("SalesTicket")；

 }

 }

 //Decorator.java文件

 publ ic abstract class Decorator extends Component{

 public void prtTicket(){

 if(myComp!=null)myComp.prtTicket()；

 }

 private (2) myComp；

 public Decorator(Component myC){

 myComp=myC；

 }

 }

 //Footer.java文件

 public class Footer extends Decorator {

 public Footer(Component myC){

  (3)；

 }

 public void prtTicket(){

  (4)；

 prtFooter()；

 }

 publ ic void prtFooter(){

 //place printing footer code here

 System.out.println("Footer")；

 }

 }

 //salesorder.java文件

 public class SalesOrder{

 void prtTicket(){

 Component myST；

 myST=new Footer( (5) )；

 //Print Ticket with footers as needed

 myST.prtTicket()；

 }

 }

(1)